Интерполяцией в Mathcad это восстановление функции по известным ее значениям или значениям ее производных в отдельных точках. Задача интерполяции экспериментальных данных сводится к тому, чтобы предсказать в промежуточных точках значение функции, заданной таблично. То есть исходные данные можно представить в виде таблицы, куда сводятся дискретные экспериментальные значения, полученные в некоторых точках наблюдений или в определенные интервалы времени. В Mathcad можно соединять табличные точки прямой линией (линейная интерполяция) либо отрезками кубического полинома (кубическая сплайн-интерполяция).
Линейная интерполяция в Mathcad реализуется посредством функции linterp(vx,vy,x), где vx, vy - векторы данных. Причём данные должны быть упорядочены по возрастанию; x - аргумент, для которого возвращается значение y
Кубическая сплайн-интерполяция позволяет провести через набор точек гладкую кривую так, чтобы в этих точках были непрерывны первая и вторая производные. Интерполяция осуществляется двумя функциями. В начале вычисляется вектор вторых производных в рассматриваемых точках, затем вычисляется значение функции в точке x -> interp(vs,vx,vy,x). Для построения вектора вторых производных в Mathcad имеется набор из 3-х функций, которые отличаются лишь граничными условиями: cspline(vx,vy) - генерирует кривую, являющуюся кубическим полиномом в граничных точках; pspline(vx,vy) - соответственно, параболу; lspline(vx,vy) - прямую.
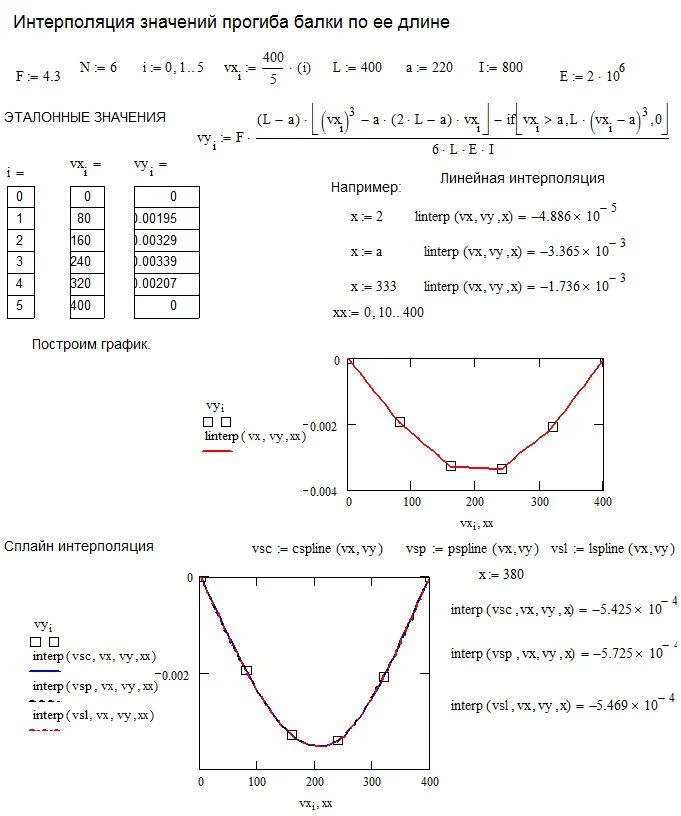
На листинге в качестве примера рассмотрена задача интерполяции значений прогиба балки по ее длине на основе шести исходных значений, полученных посредством уравнения строительной механики.
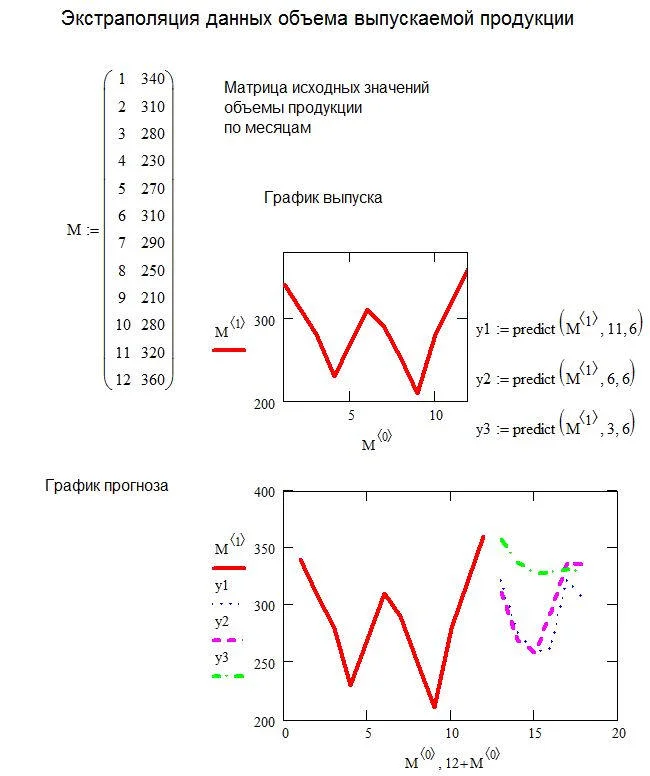
Под экстраполяцией в Mathcad понимают предсказание поведения функции за пределами области ее определения. В нашем случае эта задача сводится к определению значений некоторого параметра за пределами области, в которой значения этого параметра известны. В ближайших к правой границе точек, на основе которых производится экстраполяция в Mathcad, n - количество точек, в которых производится экстраполяция данных. Результаты, получаемые на основе функции predict(v,m,n) в значительной мере зависят от параметра m. На листинге представлены результаты работы функции на примере данных об объеме выпускаемой продукции за 12 месяцев