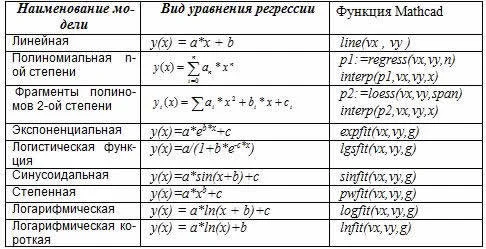
При обработке экспериментальных данных в Mathcad с целью исследования их природы, возникает необходимость выразить зависимую переменную в виде некоторой математической функции от одной или нескольких независимых переменных. Данная зависимость получила название регрессионная модель или уравнение регрессии, а методы, позволяющие получить эту зависимость, принято называть методами регрессионного анализа в Mathcad. Методы регрессионного анализа позволяют: производить расчет различного вида регрессионных моделей; проверять гипотезу адекватности модели имеющимся наблюдениям; использовать модель для прогнозирования значений зависимой переменной при новых значениях независимой переменной. В Mathcad существует набор функций, позволяющих рассчитать различные регрессионные модели. В таблице представлены функции, используемые при создании регрессионных моделей.
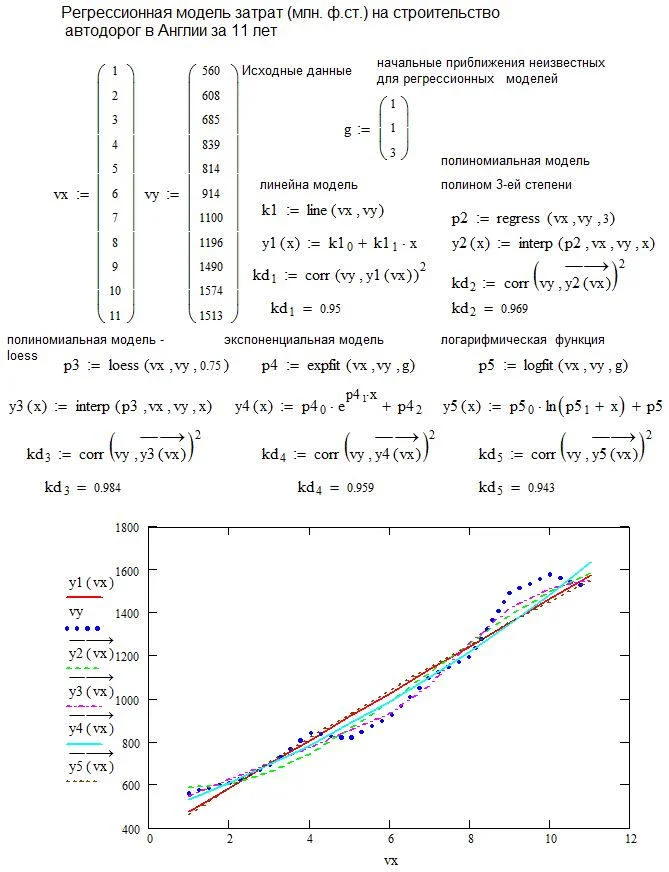
Рассмотрим суть параметров, используемых в качестве аргументов в функциях. В каждой функции в Mathcad используются два вектора исходных данных, vx - вектор независимых переменных, vy - вектор зависимых переменных. Количество элементов вектора vx и vy должно быть одинаково. Функции regress и loess используются только совместно с функцией interp. Сами функции regress и loess вычисляют только вектор, требуемый функцией interp для определения самого полинома. В Mathcad параметр span функции loess определяет величину области, на которой строится конкретный фрагмент полинома 2-ой степени. Оптимальное значение span, предлагаемое справочной системой Mathcad, равно 0.75, но в каждом конкретном случае рекомендуется путем вариантных расчетов подобрать наилучшее значение span. Параметр g является вектором начальных приближений для неизвестных функции регрессии. После определения регрессионных зависимостей в Mathcad, актуальным является выбор из их совокупности наилучшей функции, с точки зрения адекватности описания исходных экспериментальных данных. В качестве критерия, позволяющего выбрать наилучшую регрессионную модель, предлагается использовать коэффициент детерминации, численно равный коэффициенту корреляции в квадрате. Значение коэффициента корреляции в Mathcad позволяет рассчитать функция corr(A,B), где A и B – два вектора значений. На листинге , представлен пример расчета различных регрессионных моделей и выбора наилучшей из них. Как видно из данных, приведенных на листинге наилучшие результаты дает полиномиальная модель на основе функции loess. Данная модель характеризуется значением коэффициента детерминации равным 0.984.